PROBLEM?
+86 13430584894
luojunjie@piezoman.com
PAYMENT_METHOD
AD_MSG
HI_THERE!
POP_UP_MESSAGE_CONTENT
摘自麦斯塔微：抖动定义和测量
引言：
时钟抖动（jitter）是现代通信和数字系统中至关重要的性能指标之一，对数据传输速率和系统同步起着关键作用。本文将深入探讨时钟抖动的定义、不同类型，详细介绍各种抖动类型的测试方法，并分析时钟抖动对实际应用的危害。
1、时钟抖动的定义：
抖动的定义为“信号的定时事件与其理想位置之间的偏差”，时钟抖动是指时钟信号在时间上的偏差和波动。它通常以时间测量单位（如皮秒ps、飞秒fs）表示，用来描述时钟信号频率误差、相位偏移和瞬时抖动等。
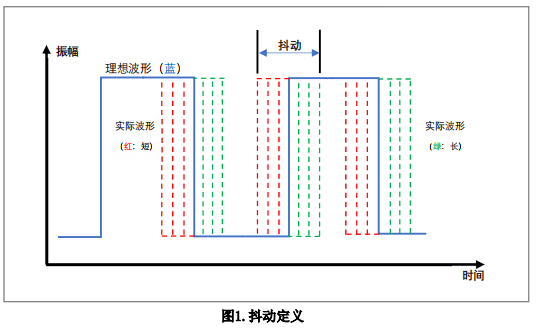
2、抖动类型
时钟信号抖动定义有多种主要是：
周期抖动 (Period Jitter）
相邻周期抖动 (Cycle to Cycle Period Jitter)
长期抖动 (Long Term Jitter)
相位抖动 (Phase Jitter)
时间间隔误差 (Time Interval Error or TIE)
2.1 周期抖动
周期抖动是时钟信号的周期时间相对于一定数量、随机选定的理想时钟信号周期的偏差。如果我们能对一定数量的时钟周期进行测量，就可以计算出这一段时间测量窗口内的平均时钟周期以及其标准偏差与峰峰值。我们通常将标准偏差和峰峰值分别称作 RMS 值和 Pk-Pk周期抖动。
Peak to Peak Period Jitter = max(Tn) – min(Tn)
RMS Period Jitter = stdEV(Tn)
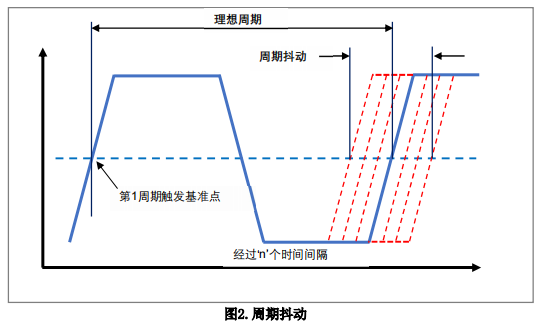
周期抖动在数字系统中的时序冗余度计算方面非常实用。例如，在一个基于微处理器的系
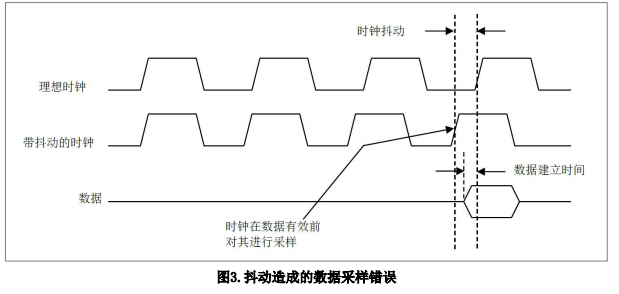
统中，处理器在时钟上升之前需要 1 ns的数据建立时间。如果时钟的周期抖动为 -2.0 ns，
则时钟的上升沿可能发生在数据有效前，因而微处理器可能得到不正确的数据。
该实例如下图所示。
2.2 相邻周期抖动
相邻周期 (C2C) 抖动，根据 JEDEC 标准 65B，是通过一定数量的相邻周期随机样本的计
算得出相邻周期的时间变化。JEDEC 标准进一步规定：每个样本的大小应大于或等于1,000。
值得注意的是，相邻周期抖动仅涉及两个连续周期之间的周期差，与理想周期无关。
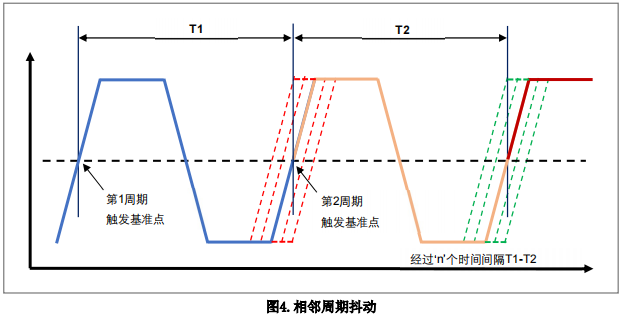
相邻周期抖动一般体现为以 ps 为单位的峰值，用于定义任意两个连续时钟上升沿之间的
最大偏差。此类型的抖动规范常用于体现扩频时钟的稳定性，因为周期抖动对频率扩展特性
更加敏感，而相邻周期抖动则不同。
2.3 长期抖动
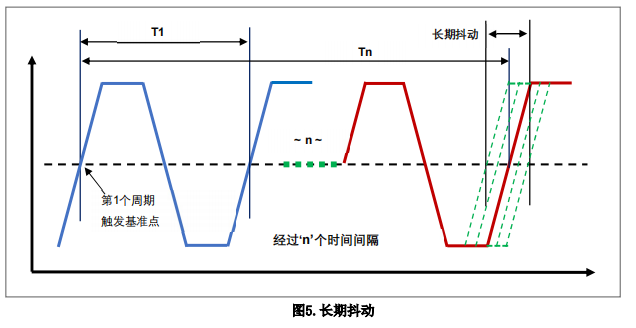
长期抖动测量的是在多个连续周期后时钟信号边沿与理想位置的变化。在实际测量中使用
的周期数量取决于不同的应用。长期抖动与周期抖动和相邻周期抖动不同，因为其代表的是
抖动在长时间间隔期间连续时钟周期流上的抖动累积效应。因此，长期抖动有时也被称为累
积抖动。长期抖动通常对图形/视频显示以及测距器等长范围遥测应用非常实用。Long-Term
jitter 测量由参考点滞后相当数量的Cycle(500-1000)后时钟沿的抖动值。该抖动参数也是
时钟稳定性的一个非常重要的指标。
2.4 相位抖动
相位噪声描述为某一给定频率偏移处的dBc/Hz 值，也称噪声频谱密度值（例如：在20KHz时为 -70 dBc/Hz，在 10MHz 时为 -105dBc/Hz），或是一段频率偏移范围内的连续曲线图。相位抖动是一定频率偏移范围内相位噪声的积分，以秒为单位表达。
在振荡器输出方波中，大部分能量均位于载波频率上。但是，部分信号能量会“泄漏到”位于载波两侧附近的频率上。相位抖动指的是相对于载波 (fc)的两个偏移频率之间包含的相位噪声能量总量。
2.5 时间间隔误差 (TIE)
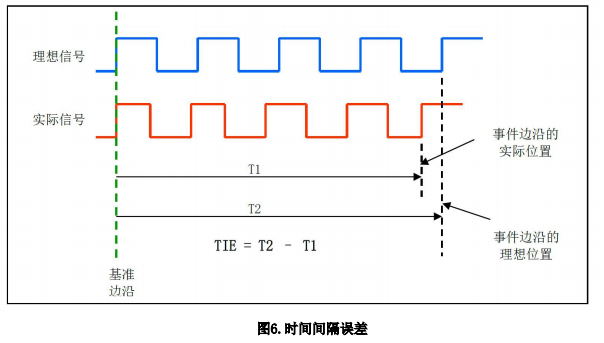
时间间隔误差 (TIE) 是指实际信号的事件边沿时间点相对于理想信号的事件边沿时间点的时间偏差。TIE 是相位噪声频谱在时域离散信号序列的表达，以秒或 ps 为单位。下图是TIE的基本概念。
理想信号通常是信号处理软件利用对实际信号周期的平均估算而得到的参考信号。
3、 抖动测试方法
3.1 测量周期抖动
1. 测量一个时钟周期的时长（上升沿至上升沿）
2. 等待随机数量的时钟周期
3. 重复上述步骤 10,000 次
4. 根据这 10,000 个样本计算平均值、标准偏差 (σ) 和峰峰值。
5. 重复上述测量 25 次。从这 25 个结果中计算平均峰峰值。
3.2 相邻周期抖动测量方法
1. 测量两个相邻时钟周期 T1 和 T2 的周期时间；
2. 计算 T1-T2 的值。记录这一数值的绝对值；
3. 等待随机数量的时钟周期；
4. 重复上述步骤 1,000 次；
5. 计算这 1,000 个样本的标准偏差 (σ) 和峰值。峰值是数据中的最大绝对值；
6. 重复上述测量 25 次，并从这 25 组结果中计算出平均峰值。
3.3 长期抖动测试方法
1. 测量 10,000 个连续时钟周期的时间间隔；
2. 等待随机数量的时钟周期；
3. 重复上述步骤 1,000 次；
4. 根据这 1,000 个样本计算平均值、标准偏差 (σ) 以及峰峰值。
FOOTER_TITLE1
FOOTER_TITLE2
FOOTER_SUB_TITLE
FOOTER_SUB_CONTENT
FOOTER_INFORMATION
©Copyright 2022 - 2024 东莞市压电侠信息技术有限公司 RESERVED |
粤ICP备2023054721号
