石英晶体谐振器和振荡器 频率控制和定时应用教程(之四）

Allan偏差

也称为双样本偏差，或“艾伦方差”的平方根，它是描述时域中振荡器短期稳定性的标准方法。用σy（τ）表示，

where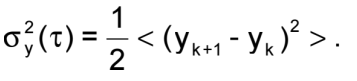       

分数频率是在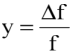一段时间内测量的

间隔，τ；（yk+1-yk）是成对的

y的连续测量，理想情况下，<>表示无穷多（yk+1-yk）2的时间平均值。通过有限数量的m次测量可以获得一个很好的估计

（m≥100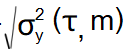）。通常表示·，即。

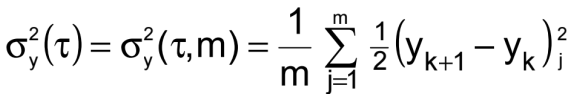
为什么σy（τ）？

经典方差：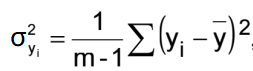

一些常见的噪声发散

随机游走等过程，即方差随着数据点数量的增加而增加。

l艾伦方差：

•精密振荡器中观察到的所有噪声过程的收敛。

•与幂律谱密度类型有直接关系。

•易于计算。

•在估计噪声过程方面比快速傅里叶变换更快、更准确。

频率噪声和σy（τ）

时域稳定性

*为了使σy（τ）成为随机频率波动的适当度量，必须从长τ的数据中适当地减去老化。

σy（τ）的幂律依赖性

在频率噪声闪烁（即“闪烁基底”）区域以下，晶体振荡器通常表现出τ-1（白相位噪声）依赖性。原子

标准显示τ-1/2（白频噪声）依赖性低至约

伺服回路时间常数，τ-1依赖性小于该时间常数。

闪烁下限开始时的典型τ为：晶体振荡器为1s，晶体振荡器为103s

Rb标准和Cs标准的105s。在τ较大的情况下，频率和老化的随机游走占主导地位。

噪音图片

图表显示了量z（t）的波动，例如，可以是计数器的输出（Δf vs.t）或相位检测器的输出（φ[t]vs.t。这些图显示了模拟的时域行为

对应于最常见的（幂律）光谱密度；hα是振幅

系数。注：由于SΔf=f2Sφ，例如白频噪声和相位随机游走是等效的。

谱密度

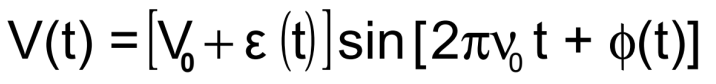
在频域中，由于相位偏差φ（t），一些

功率在ν0以外的频率。稳定性为

以“光谱密度”为特征。光谱密度SV（f）

在以f为中心的单位带宽内，均方电压<V2（t）>不是衡量频率稳定性的好方法，因为ε（t）和φ（t）都对频率稳定性有贡献，而且它与频率波动没有唯一关系

（尽管ε（t）在精密频率源中通常可以忽略不计。）

相位和分数频率波动的谱密度Sφ（f）和Sy（f）分别用于测量

频域。量g（t）的谱密度Sg（f）是以f为中心的单位带宽中g（t的均方值。此外，

带宽BW中g2的RMS值由下式给出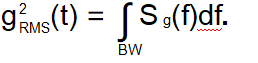

混音器功能

相位检测器

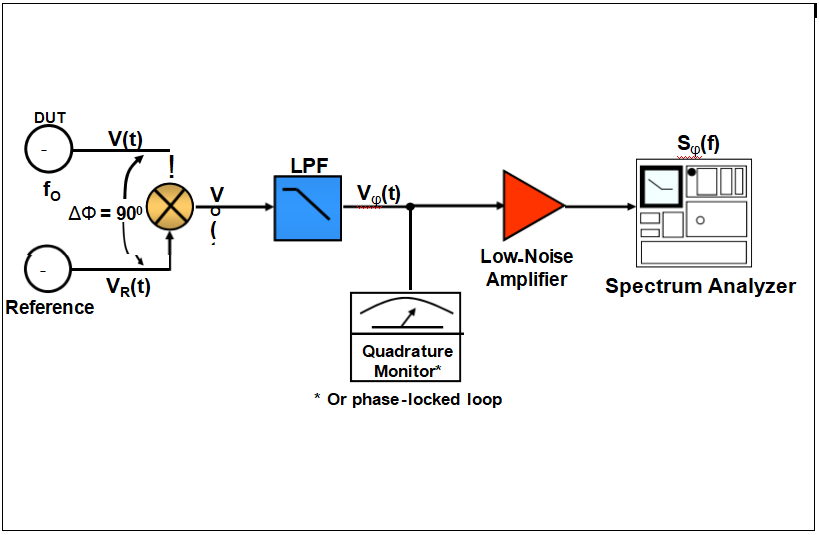
相位噪声测量

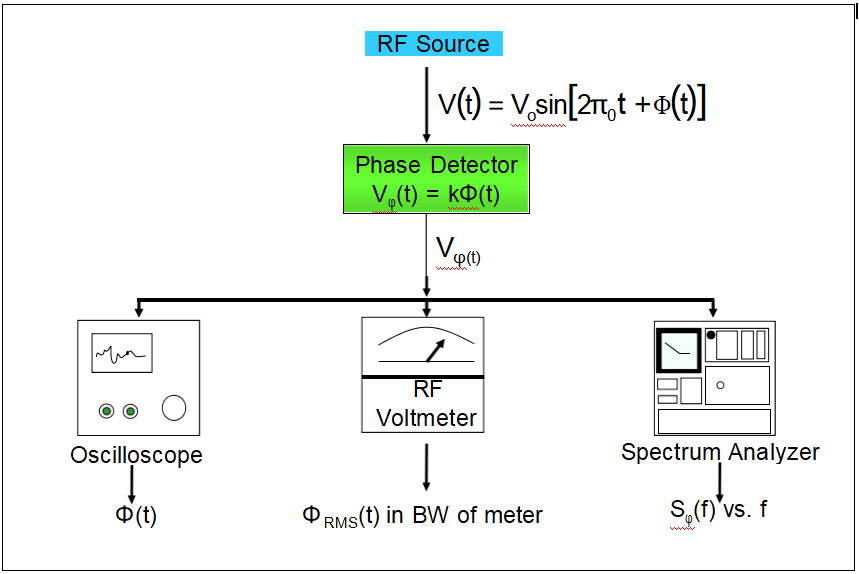
频率-相位-时间关系

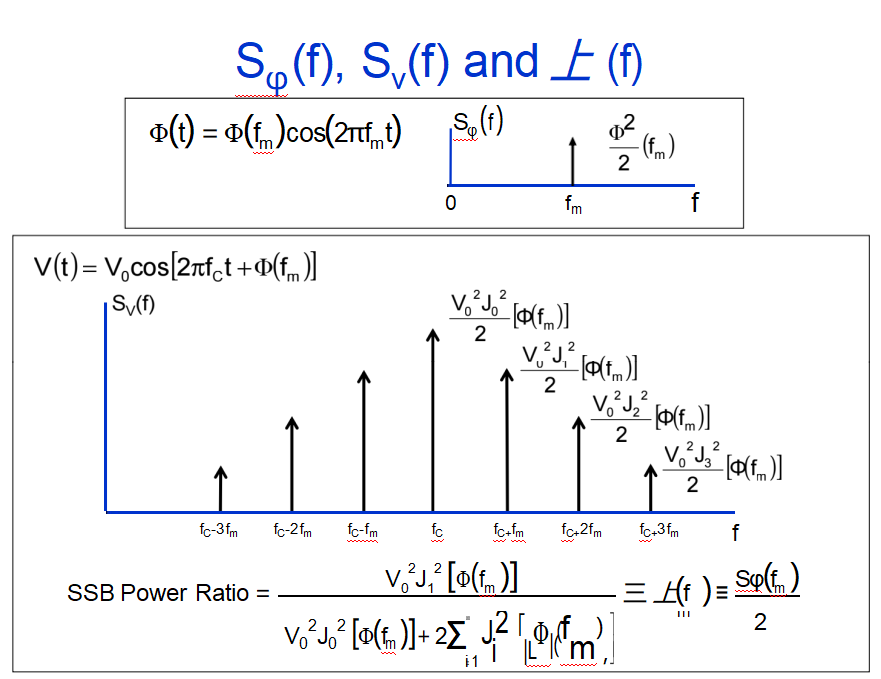
相位噪声的类型

晶体振荡器中的噪声

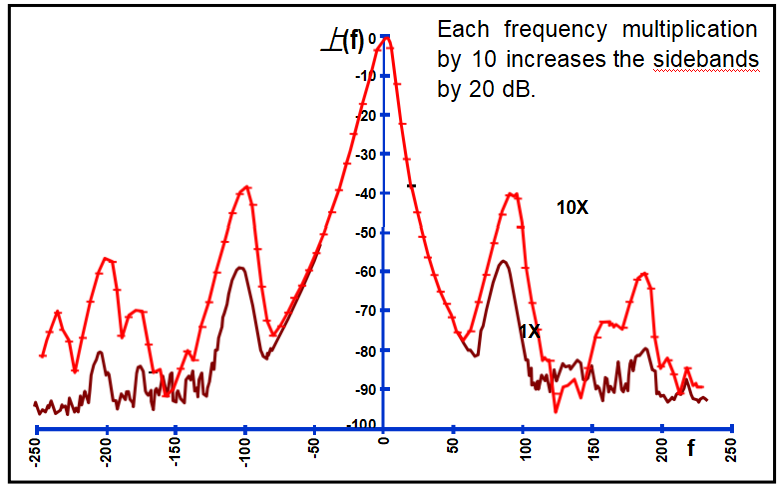
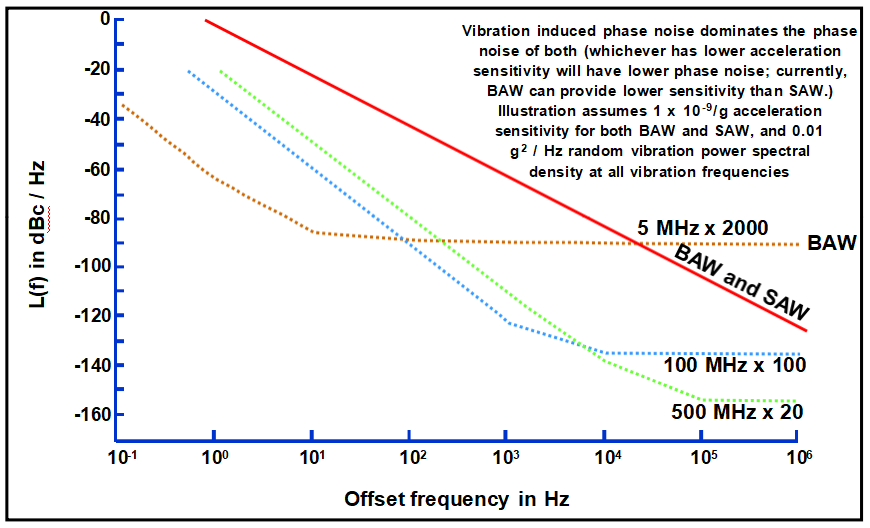
l频率乘以N会使相位噪声增加N2（即增加20log N，单位为dB）。

l在许多应用中，振动引起的“噪声”主导了所有其他噪声源（见后面的加速度效应部分）。

l靠近载波（在谐振器的BW内），Sy（f）变化为1/f，Sφ（f）为1/f3，其中f=与载波频率的偏移，ν。Sφ（f）也随1/Q4变化，其中Q=无负载Q

l Qmaxν=常数。，Sφ（f）≠ν4。（Qmaxν）BAW=1.6 x 1013赫兹；（Qmaxν）声表面波=1.05 x 1013赫兹。

σy（τ）随τ-1和τ-1/2变化的区域（τ-1/2出现在原子频率标准中），

σy（τ）├（QSR）-1，其中SR是信噪比；即，Q和信噪比越高，短期稳定性越好（频域中远离载波的相位噪声也越好）。

l当振荡器维持电路是一个重要的噪声源时，谐振器的负载Q会影响噪声。

噪声基底受约翰逊噪声的限制；噪声功率，kT=-174 dBm/Hz，290K

l更高的信号电平可以改善噪声基底，但不能改善近距离噪声。（事实上，高驱动电平通常会降低近距离噪声，原因尚不完全清楚。）

l低噪声SAW与低噪声BAW相乘：BAW在f<~1kHz时噪声较低，SAW在f>~1kHz时噪音较低；可以对两者进行锁相，以获得两者的最佳效果。

低噪声SAW和BAW倍增至10 GHz

（在非振动环境中）

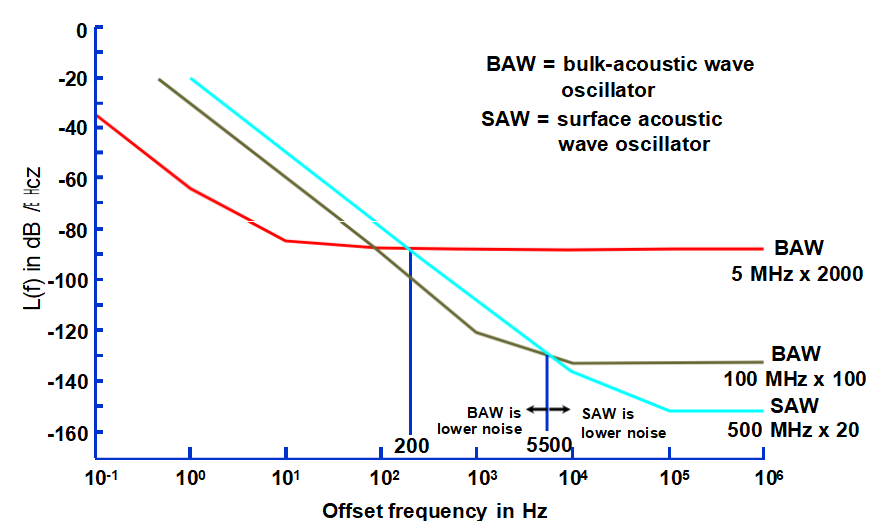
低噪声SAW和BAW倍增至10 GHz

（在振动环境中）

TCXO噪声

TCXO的短期稳定性取决于温度（T），通常比OCXO差，原因如下：

•TCXO晶体的频率（f）与T的斜率随T而变化。例如，在~20℃时，f与T的坡度可能接近零，但在T的极端值时，它将为~1ppm/oC。T

波动将在实验室环境T下引起较小的f波动，因此稳定性可能很好，但毫度波动将在T极值处引起~10-9 f波动。TCXO的f与T斜率也随T而变化；零点和最大值可以在任何T处

最大斜率约为1ppm/oC。

•AT切割晶体的热瞬态敏感性使T波动的影响不仅取决于T，还取决于T的变化率（而SC切割晶体

通常用于精密OCXO对热瞬变不敏感）。在变化的T条件下，T传感器（热敏电阻）和晶体之间的T梯度会加剧问题。

•TCXO通常使用基模AT切割晶体，其Q值低于OCXO中通常使用的晶体，C1值大于OCXO中使用的晶体。Q越低，晶体本身就越嘈杂，而C1越大，振荡器对电路噪声越敏感。

•AT切割晶体的f与T通常表现出活性下降（见本文后面的“活性下降”

第章）。在出现骤降的T处，f与T的斜率可能非常高，因此T波动引起的噪声也会非常高，例如，σy（τ）可能降低100倍，相位噪声可能降低30 dB。任何T点都可能出现活动下降。

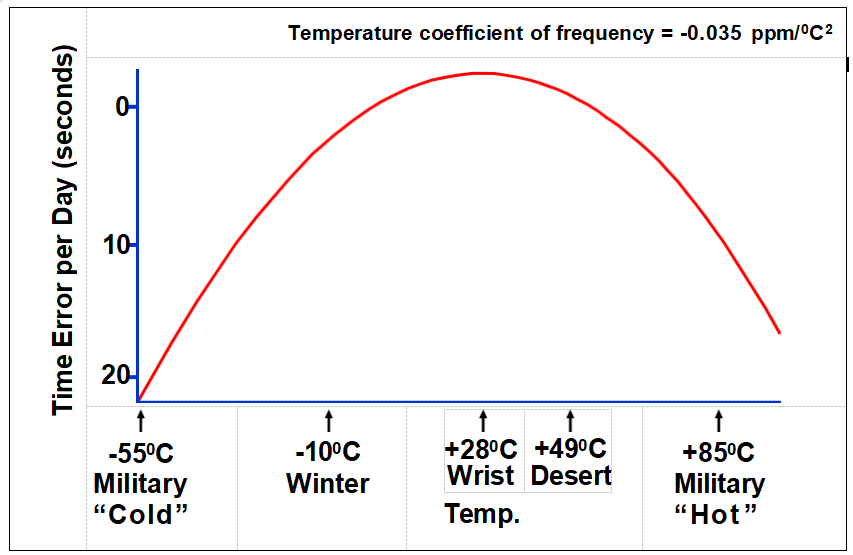
石英手表精度与温度

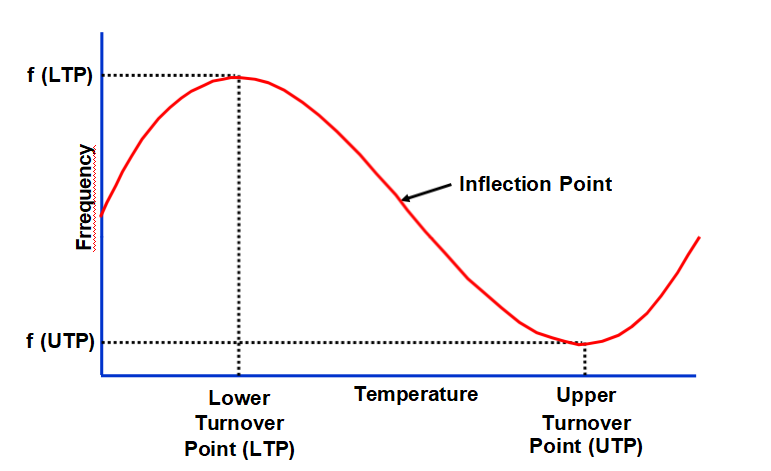
频率与温度特性

谐振器f与T的决定因素

主要：切割角度

l中学：

•Overtone

•空白几何形状（轮廓、尺寸比）

•材料杂质和应变

•安装和粘合应力（大小和方向）

•电极（尺寸、形状、厚度、密度、应力）

•驾驶水平

•干扰模式

•负载电抗（值和温度系数）

•温度变化率

•热历史

•电离辐射

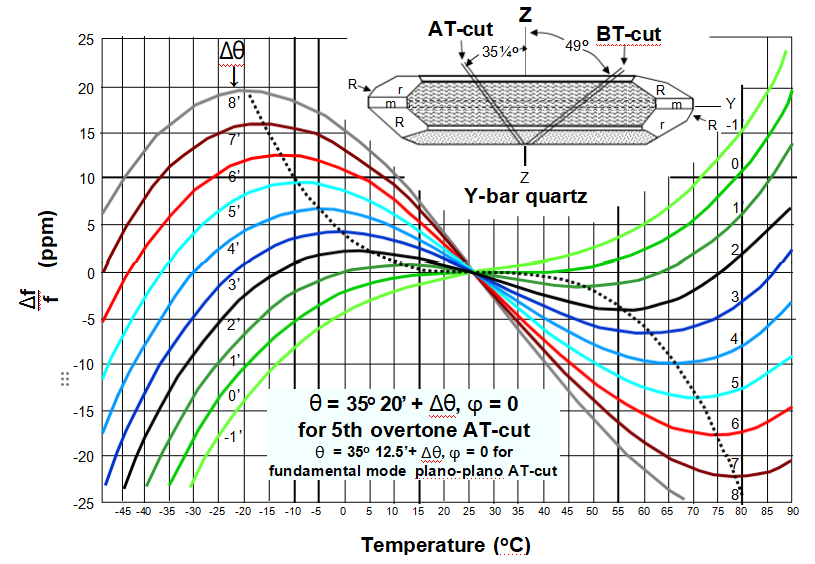
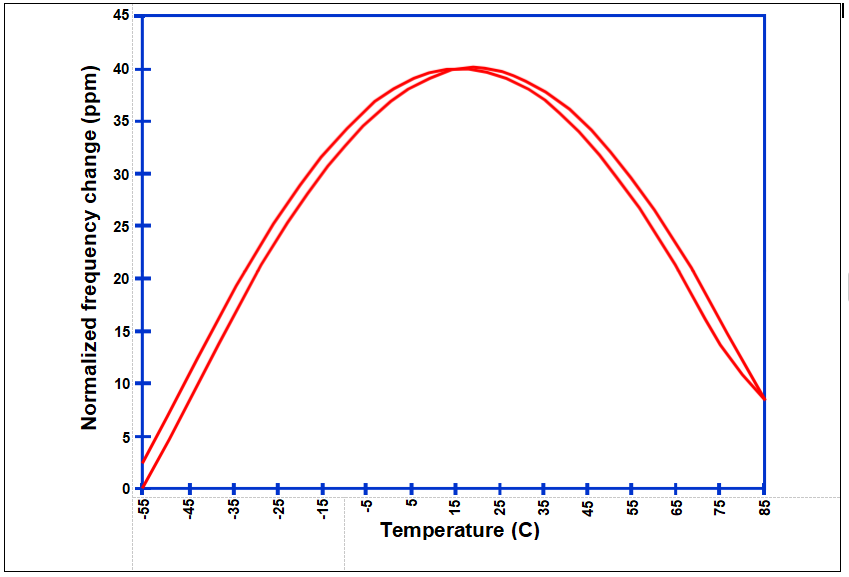
频率温度与切割角度，AT切割

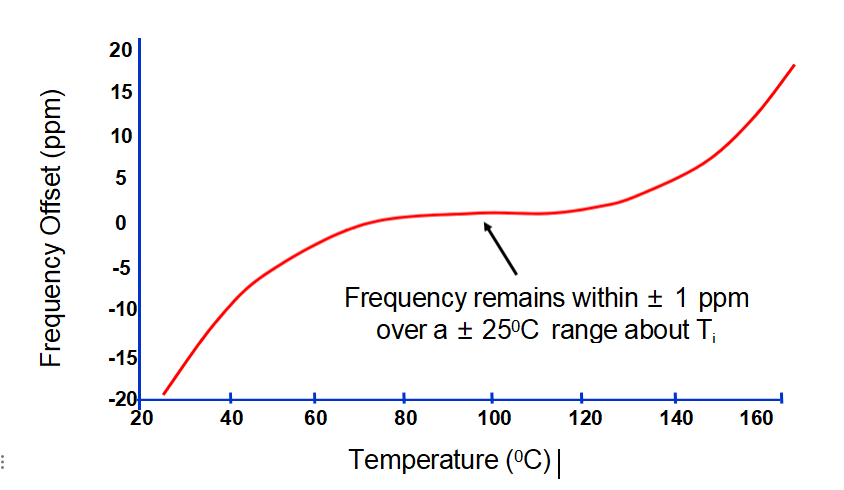
OCXO应用中SC截止谐振器的期望f与T

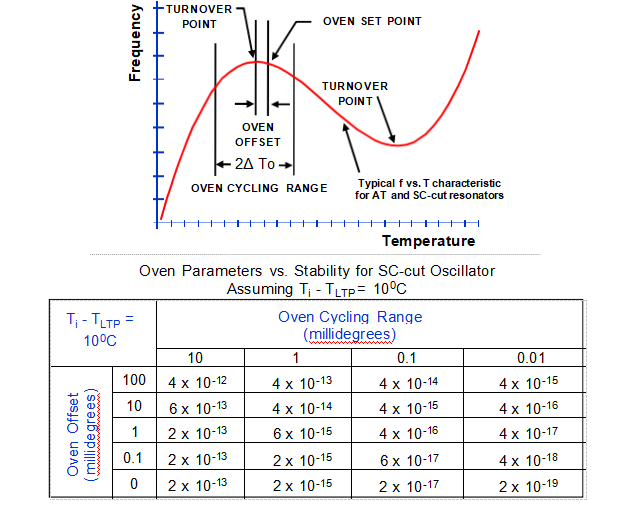
OCXO烘箱对稳定性的影响

AT和其他非热瞬态补偿振荡器切割的比较表没有意义，因为动态f与T效应通常会主导静态f与T效果。

烘箱稳定性限制

•通过前馈补偿技术实现了105的热增益（即，在外壳T外测量并调整热敏电阻的设定值以进行预测和

补偿），并配有双烤箱。例如，当增益为105时，如果外部ΔT=100oC，内部ΔT=1 mK。

•良好放大器的稳定性~1μK/K

•热敏电阻的稳定性约为1mK/年至100mK/年

•噪声<1μK（热敏电阻中的约翰逊噪声+放大器噪声+桥电流中的散粒噪声）

•温度波动的量子极限~1nK

•最佳的烤箱设计可以提供非常高的f与T稳定性

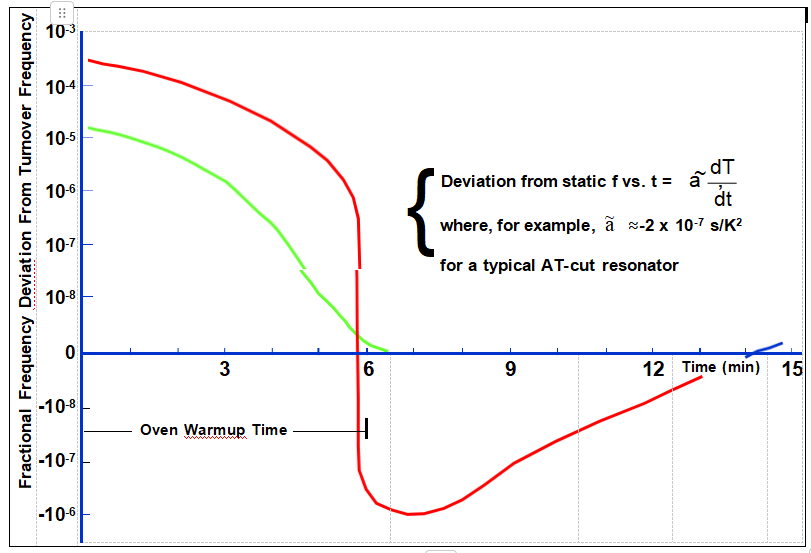
AT和SC切割谐振器的预热

TCXO热滞后

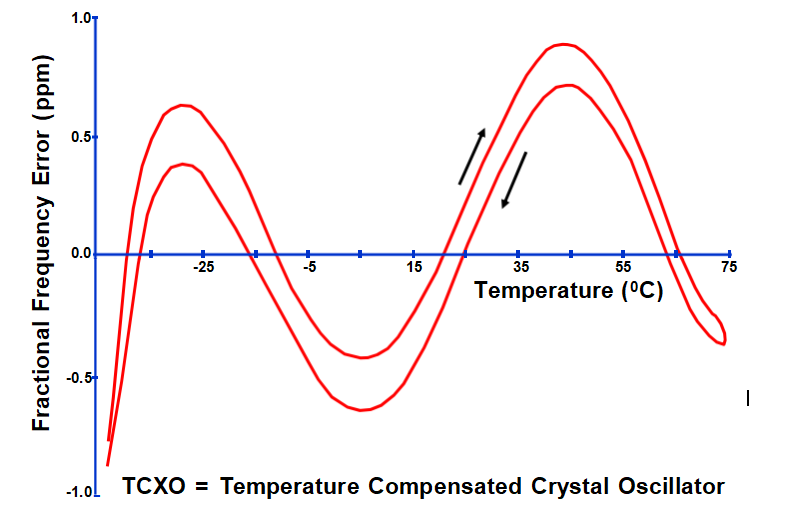
明显滞后

OCXO收回

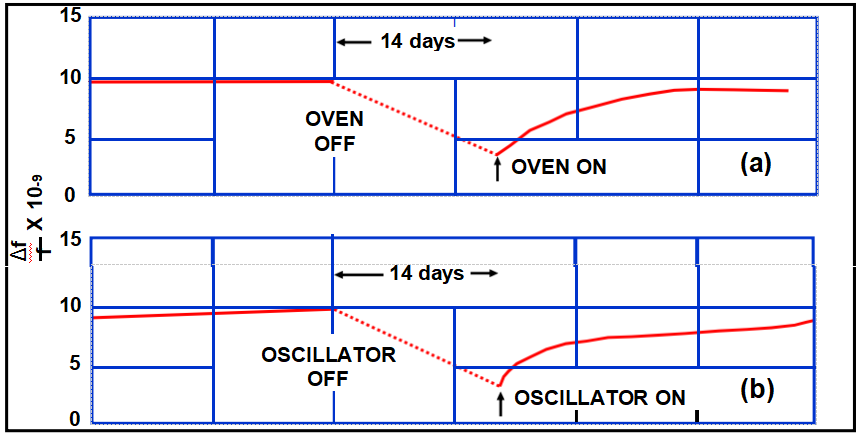
在（a）中，振荡器在烤箱关闭和打开的同时持续打开。在（b）中，烤箱在振荡器关闭和打开时持续打开。

TCXO微调效果

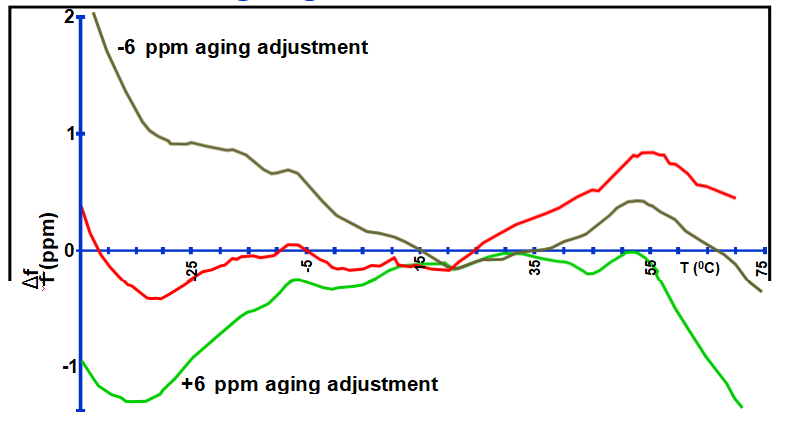
在TCXO中，温度敏感电抗用于补偿f与T的关系

变化。可变电抗也用于补偿TCXO老化。老化调整对f与T稳定性的影响是“微调效应”。曲线显示f与T

零微调和±6ppm微调时“0.5ppm TCXO”的稳定性。（为清楚起见，曲线已垂直位移。）

为什么有修剪效果？

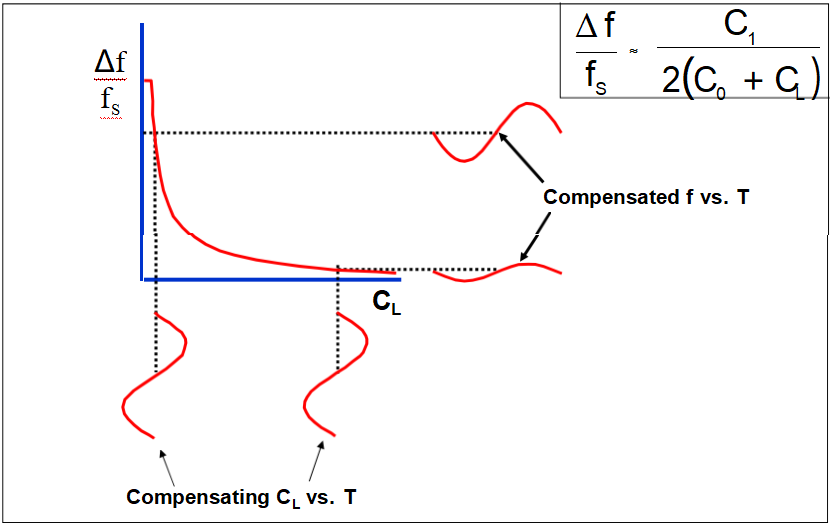
负载电容对f与T的影响

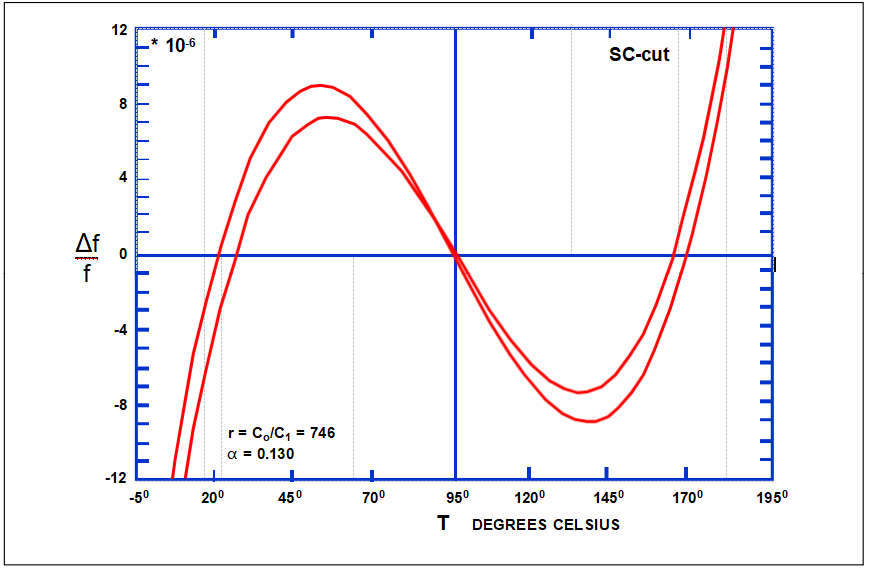
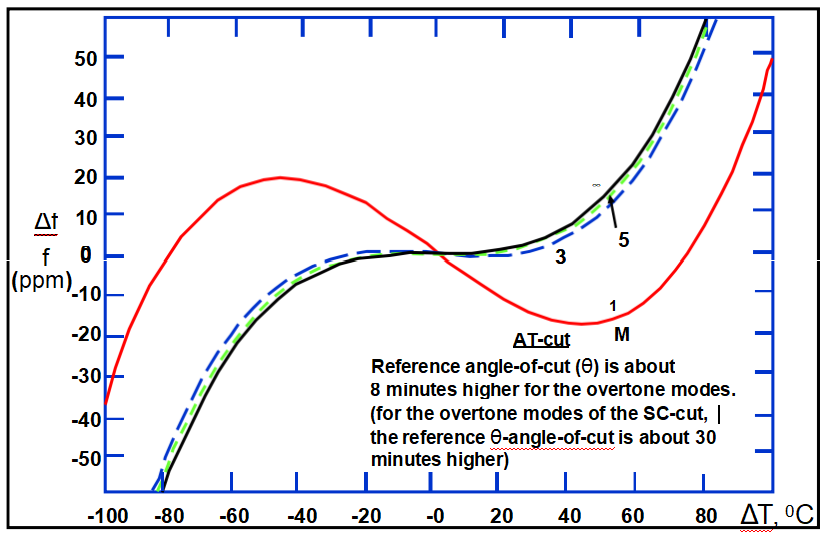
谐波对f与T的影响

幅频效应

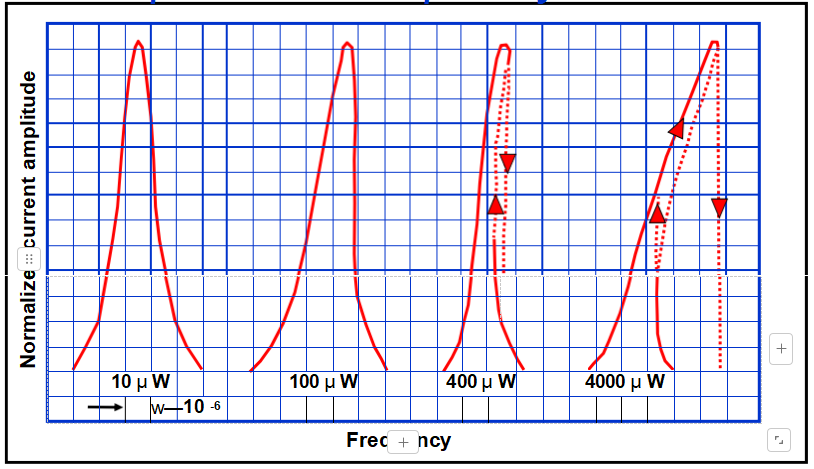
在高驱动水平下，由于石英的非线性，共振曲线变得不对称。

频率与驱动电平

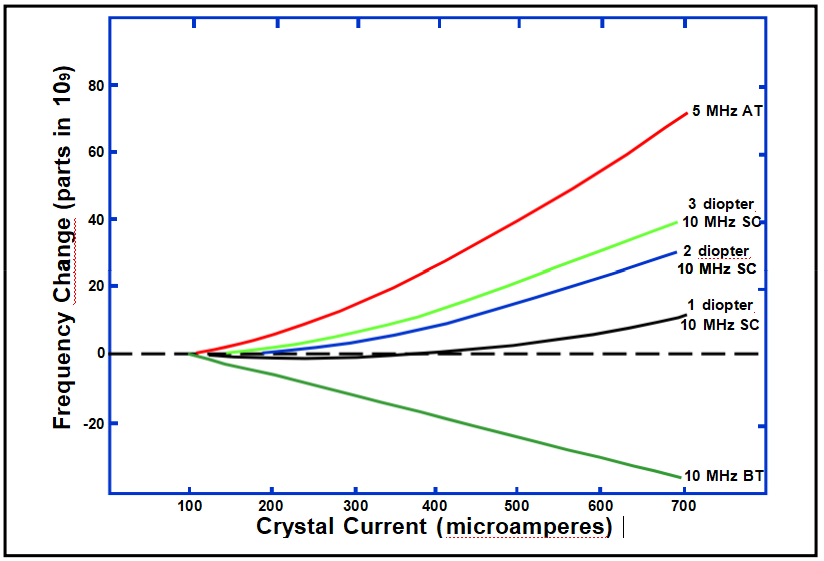
驱动水平与阻力

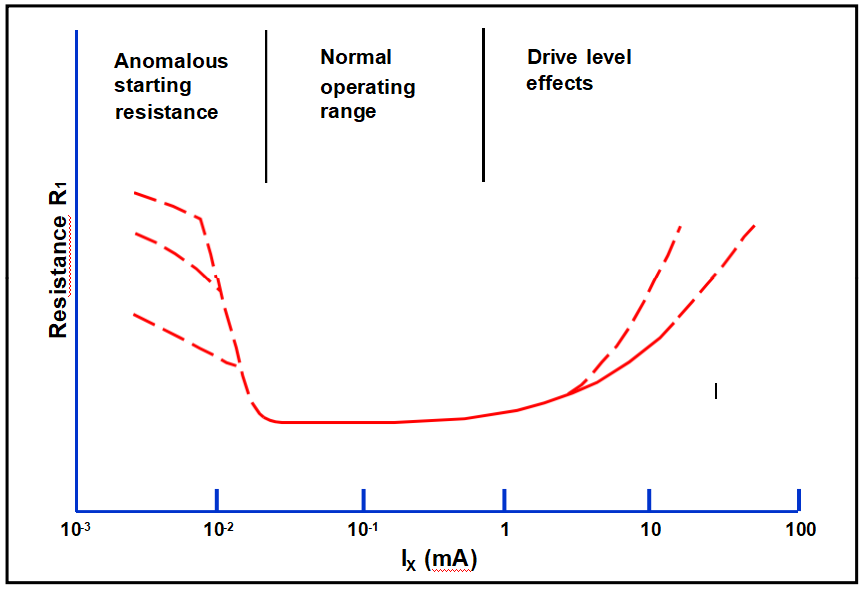
第二级驱动效应

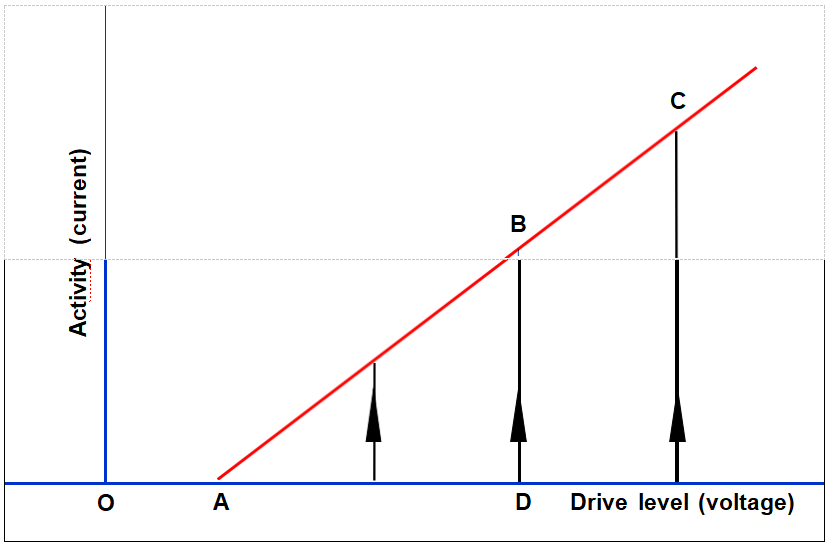
活动下降

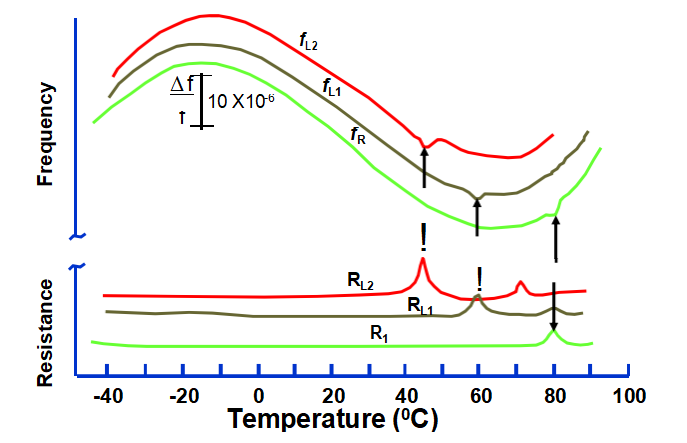
在有负载和无负载运行时，f与T和R与T的活动下降

电容器。浸入温度是CL的函数，这表明浸入是由具有较大负温度系数的模式（可能是弯曲）引起的。

频率跳跃

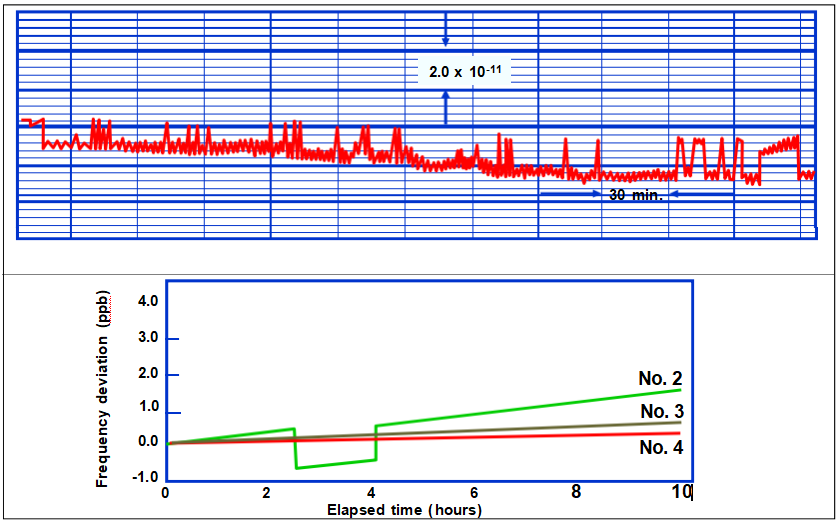
加速度与频率变化

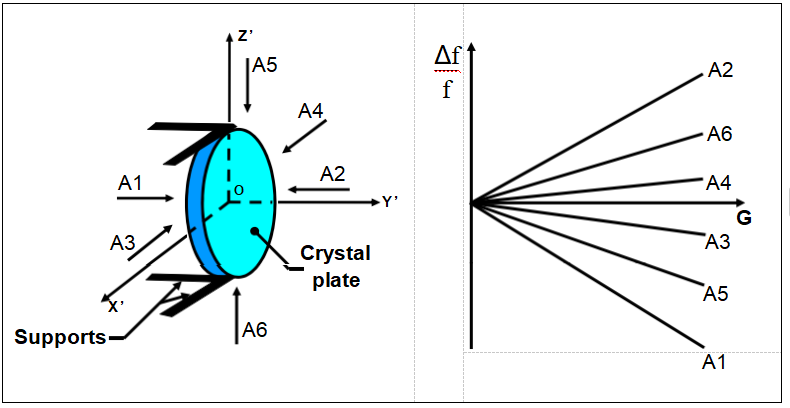
频率偏移是幅度和方向的函数

并且通常与高达至少50gs的幅度呈线性关系。

加速无处不在

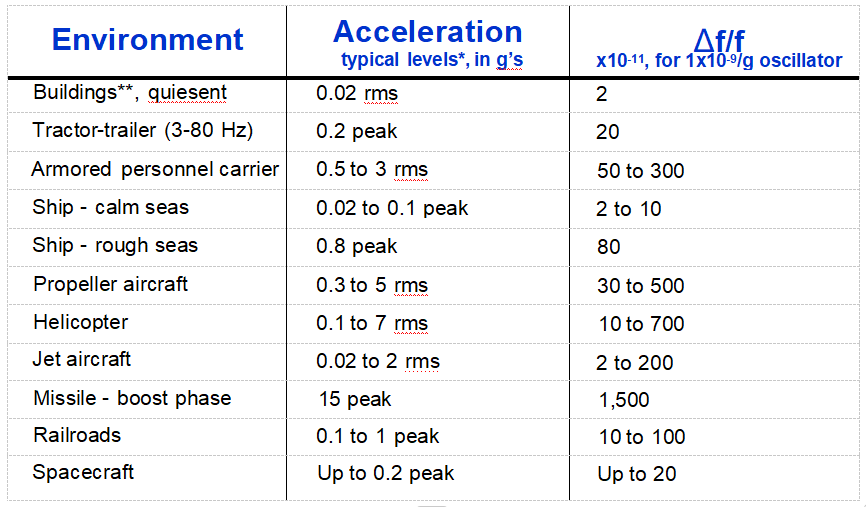
*振荡器的水平取决于振荡器的安装方式和位置。平台共振可以大大放大加速度水平。

**建筑物振动会对噪声测量产生重大影响

加速影响“一切”

•加速力变形（应变）

材料和器件特性的变化——在某种程度上

•示例：

-石英谐振器频率

-放大器增益（应变改变半导体带结构）

-激光二极管发射频率

-光学性能.光纤折射率（声光）

-腔频率

-DRO频率（应变改变介电常数）

-原子钟频率

-杂散电抗

-时钟速率（相对论效应）

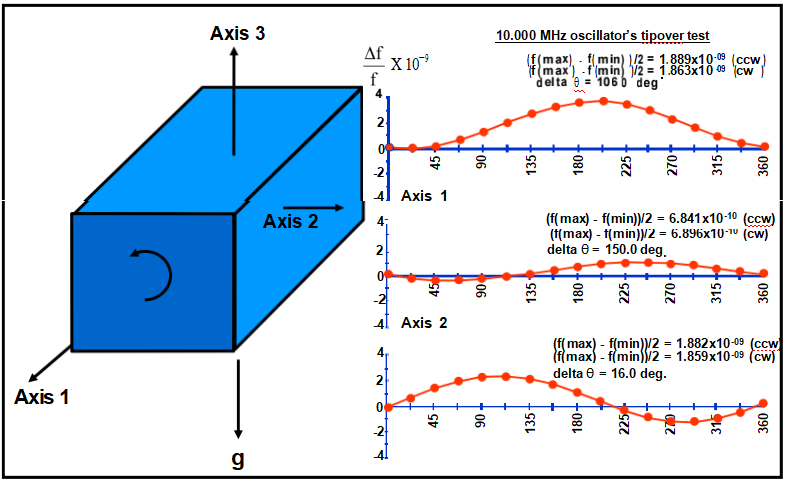
2-g倾翻试验

（Δf与绕三个轴的姿态）

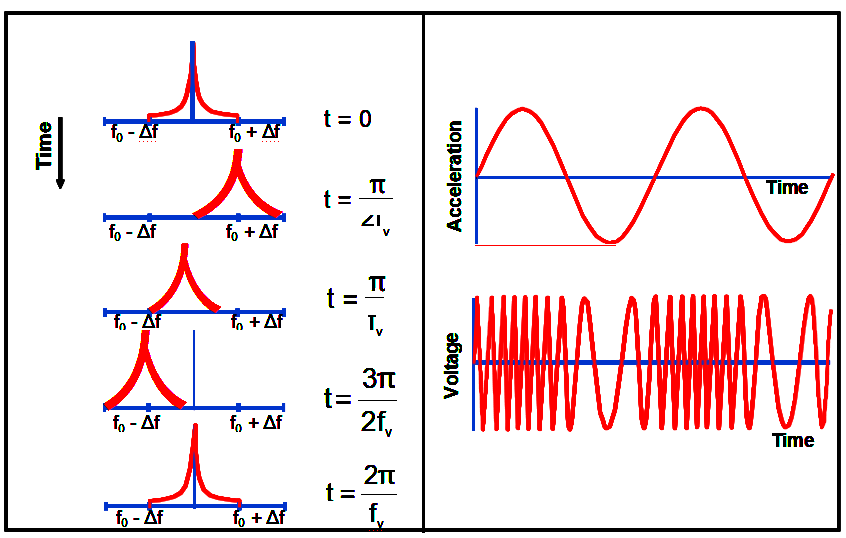
正弦振动调制频率

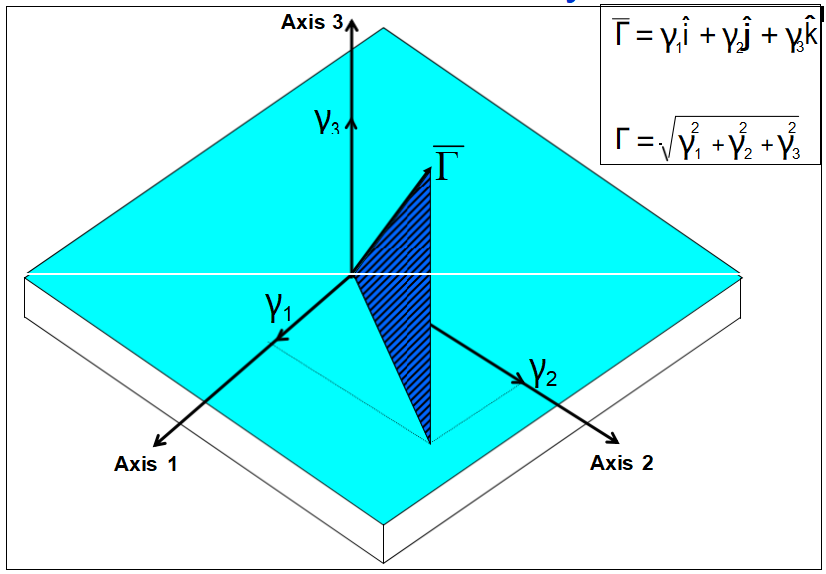
加速度灵敏度矢量

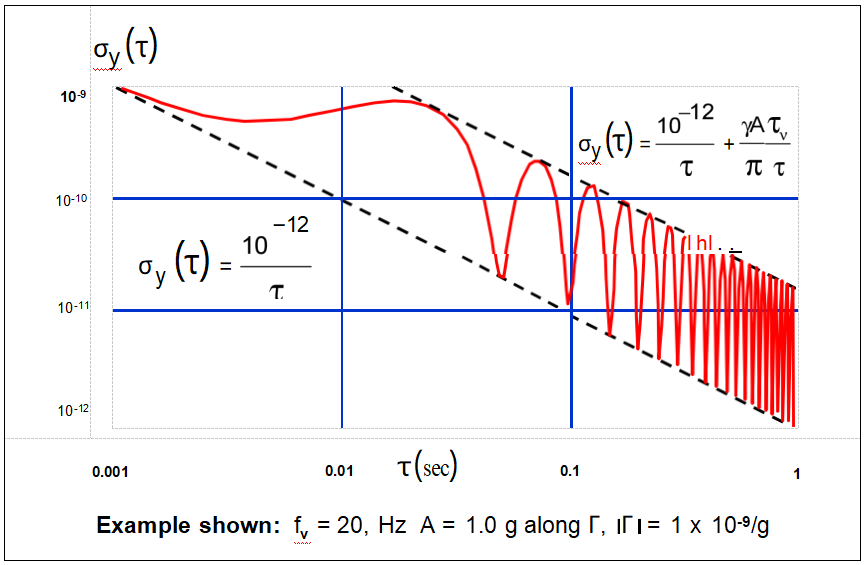
振动引起的艾伦偏差退化

振动引起的相位偏移

振动调制信号的相位为

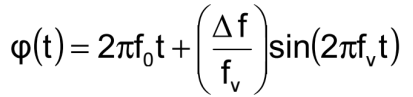
当振荡器受到正弦振动时，峰值相位偏移为

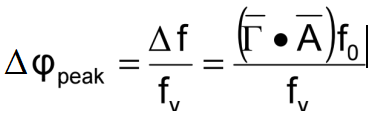
示例：如果10 MHz，1 x 10-9/g振荡器受到10 Hz的影响

振幅为1g的正弦振动，峰值振动引起的相位偏移为1×10-3弧度。如果将此振荡器用作参考

10GHz雷达系统中的振荡器，10GHz处的峰值相位偏移将为1弧度。如此大的相位偏移可能是灾难性的

例如采用锁相环（PLL）或相移键控（PSK）的那些系统的性能。

振动引起的边带

倍频后振动引起的边带